Mobility for Matrices

Contingency Tables

• The primative representation of data for mobility
• These data illustrate the single period case

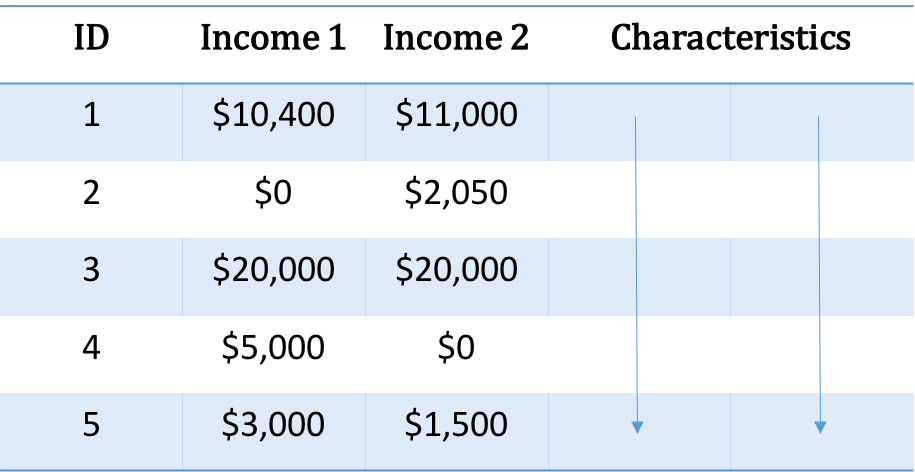
Contingency Tables

• The primative representation of data for mobility
• These data illustrate the single period case
• We may discretize income either into bins of a fixed width or into quantiles

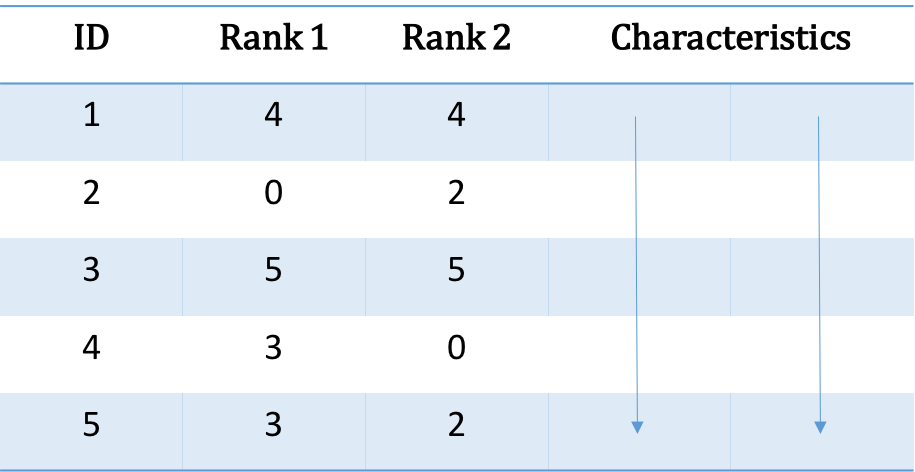
Transition Matrices

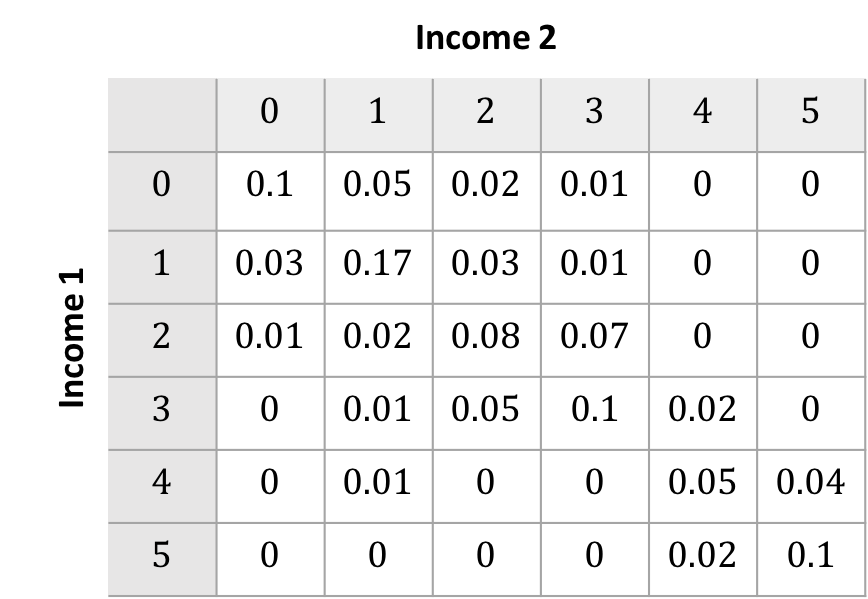
• Construct the count matrix by binning observations to the cartesian product of the ranks

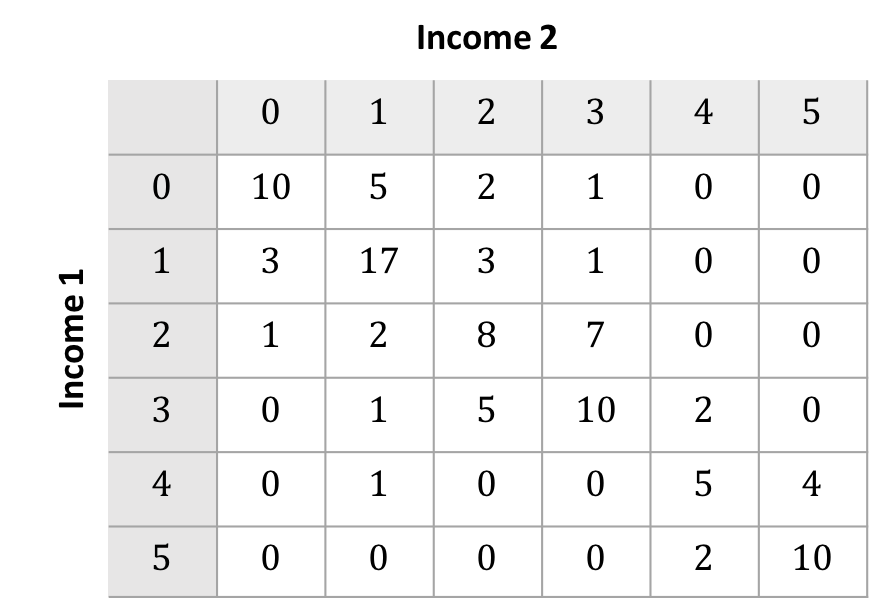
Transition Matrices

• Construct the count matrix by binning observations to the cartesian product of the ranks
• Construct the unconditional transition matrix $M_u$ by dividing each cell by the total observations

Transition Matrices

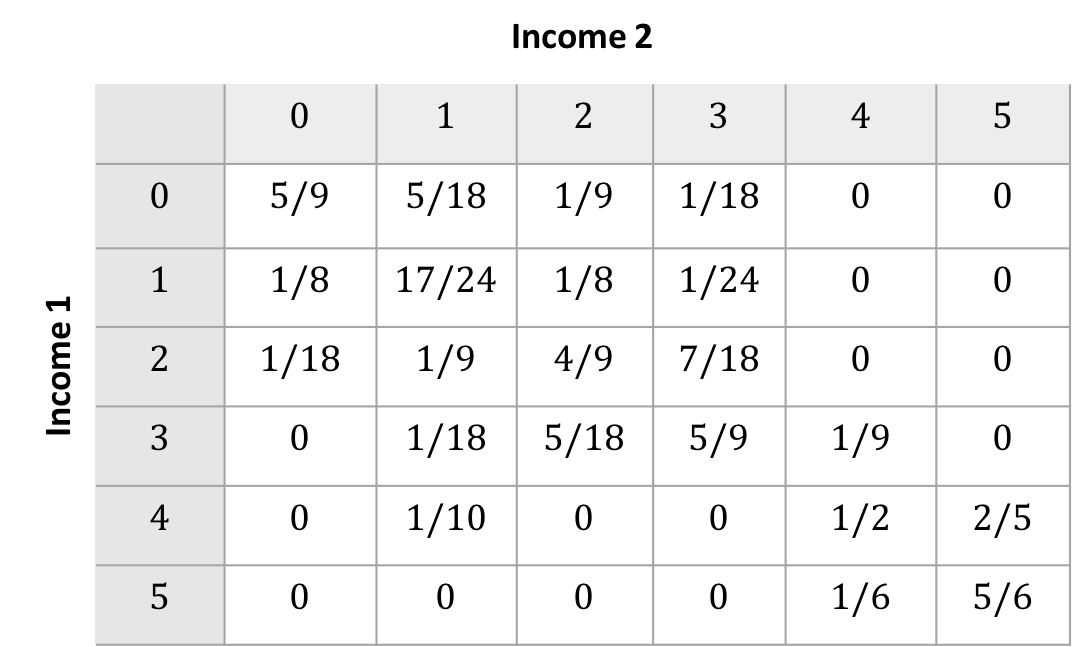
• Construct the count matrix by binning observations to the cartesian product of the ranks
• Construct the unconditional transition matrix $M_u$ by dividing each cell by the total observations
• Alternatively, the conditional transition matrix $M_c$ can be used to take advantage of stochatic properties

Mobility Indices

Prais-Bibby Index

• Let $n$ denote the number of ranks


• $m_{PB}(M_c) = \left( \sum_{i = 1}^N (1 - M_{cii})\sum_{j = 1}^N M_{uij} \right)$


• Captures the probability that one moves from their initial rank

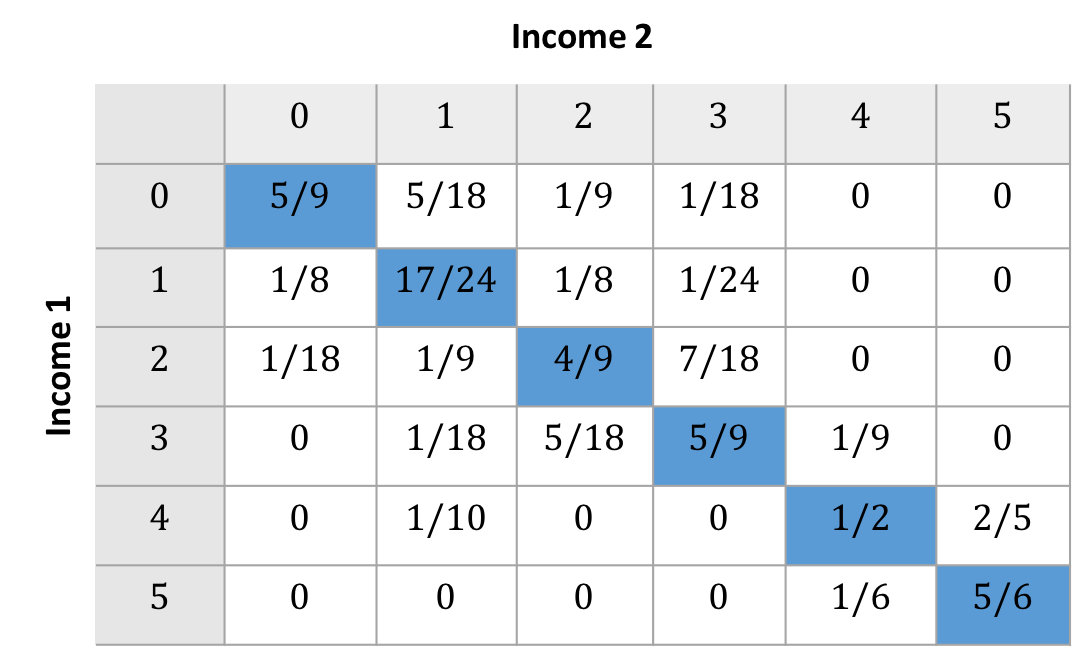
$m_{PB}(M_c) = 0.4$

Prais-Bibby Index

• Let $n$ denote the number of ranks


• $m_{PB}(M_c) = \left( \sum_{i = 1}^N (1 - M_{cii})\sum_{j = 1}^N M_{uij} \right)$


• Captures the probability that one moves from their initial rank


• Equivalent to one minus the sum of the diagonal of $M_u$

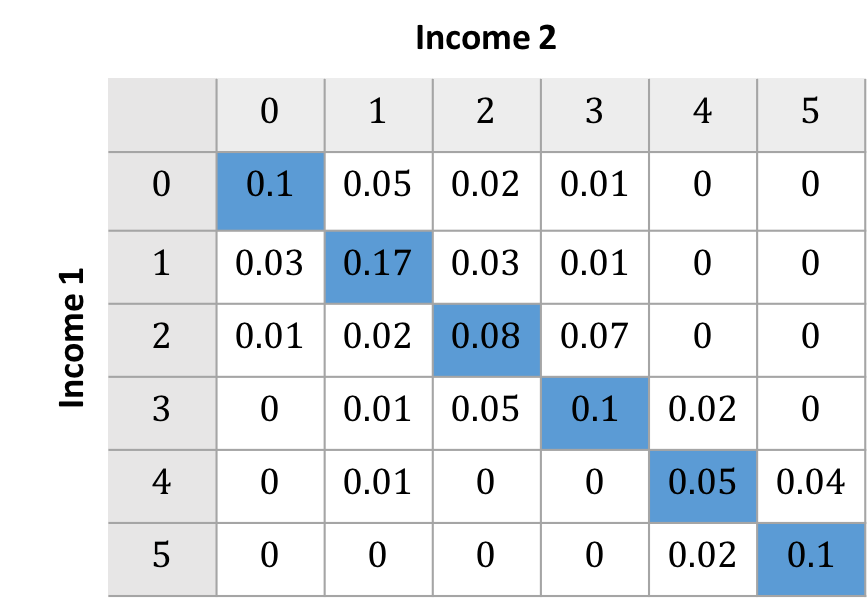
$m_{PB}(M_c) = 0.4$

Mobility Indices

• $m_{PB}$ is an individualistic discrete index
• An index is individualistic if each individual in the same makes a marginal contribution to the index
• An index is discrete if it measures whether an individual experienced mobility rather than the magnitude of the mobility

Mobility for Arrays

Contingency Tables

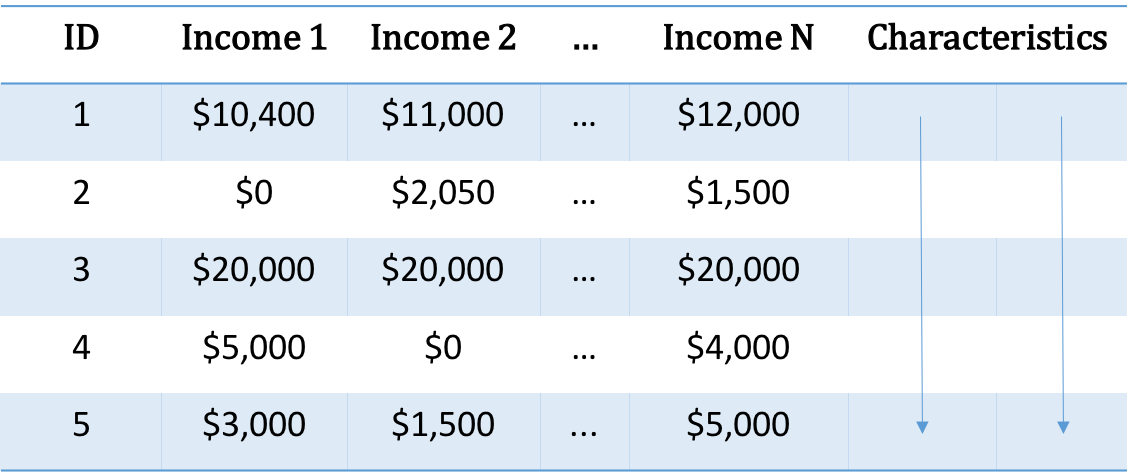
Contingency Tables

Multidimensional Arrays

• Analgous stucture to a transition matrix
• For $N = 3$, the array can be visualized as a cube
• Follows process of computing the count array, unconditional transition array, and conditional transition array

Indices for Multidimensional Arrays

• We can generalize the Prais-Bibby Index to arbitrary arrays as follows: let $m_{PB}:\mathcal{A} \rightarrow \mathbb{R}$, where $\mathcal{A}$ is the set of square transition arrays
• The function is defined as before where the trace or diagonal of the array is the set of cells that each share the same index on each dimension
• Interpretation: one does not experience mobility if one is in the same rank at each observed time

The Case of Noisy Data

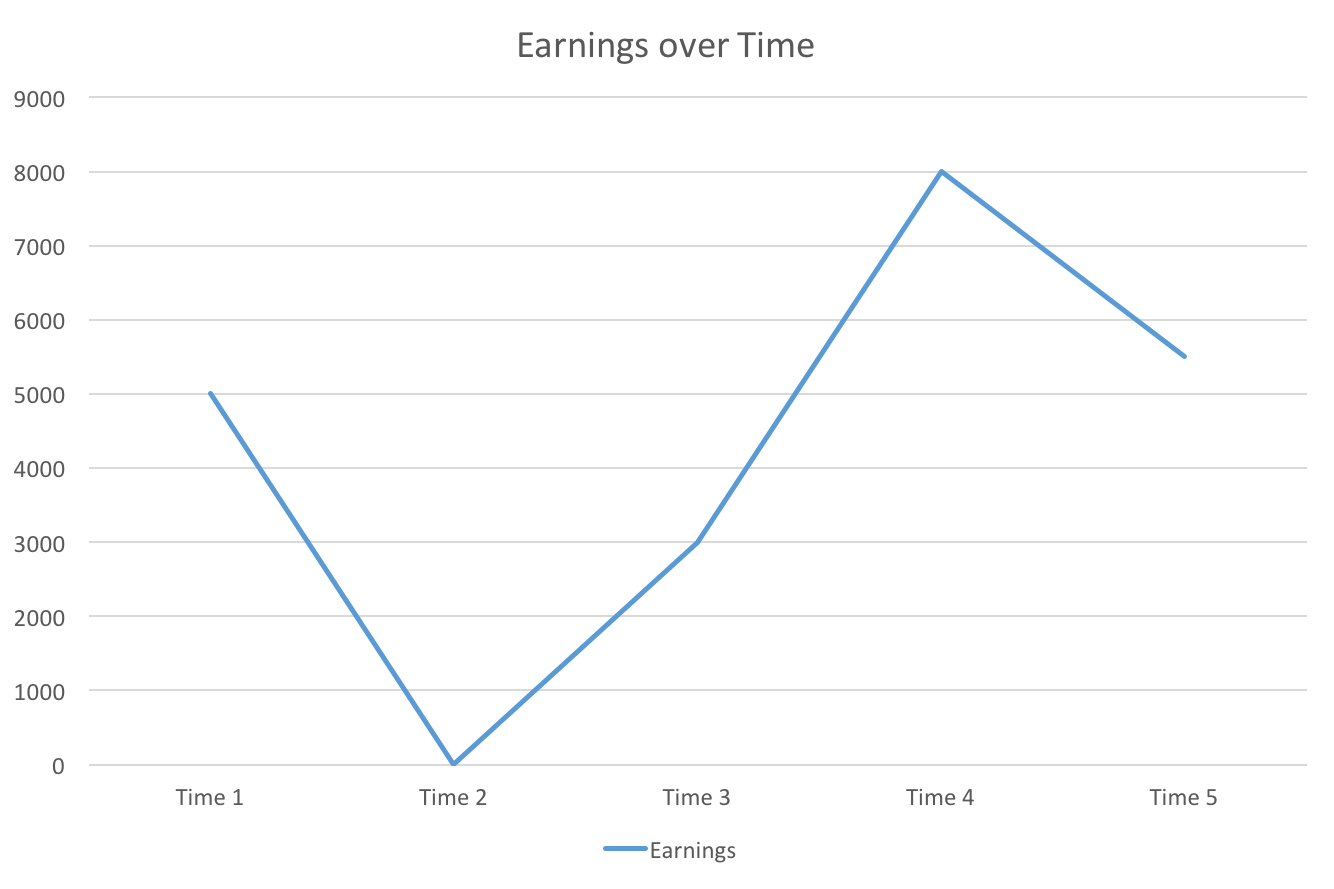
Noisy Data

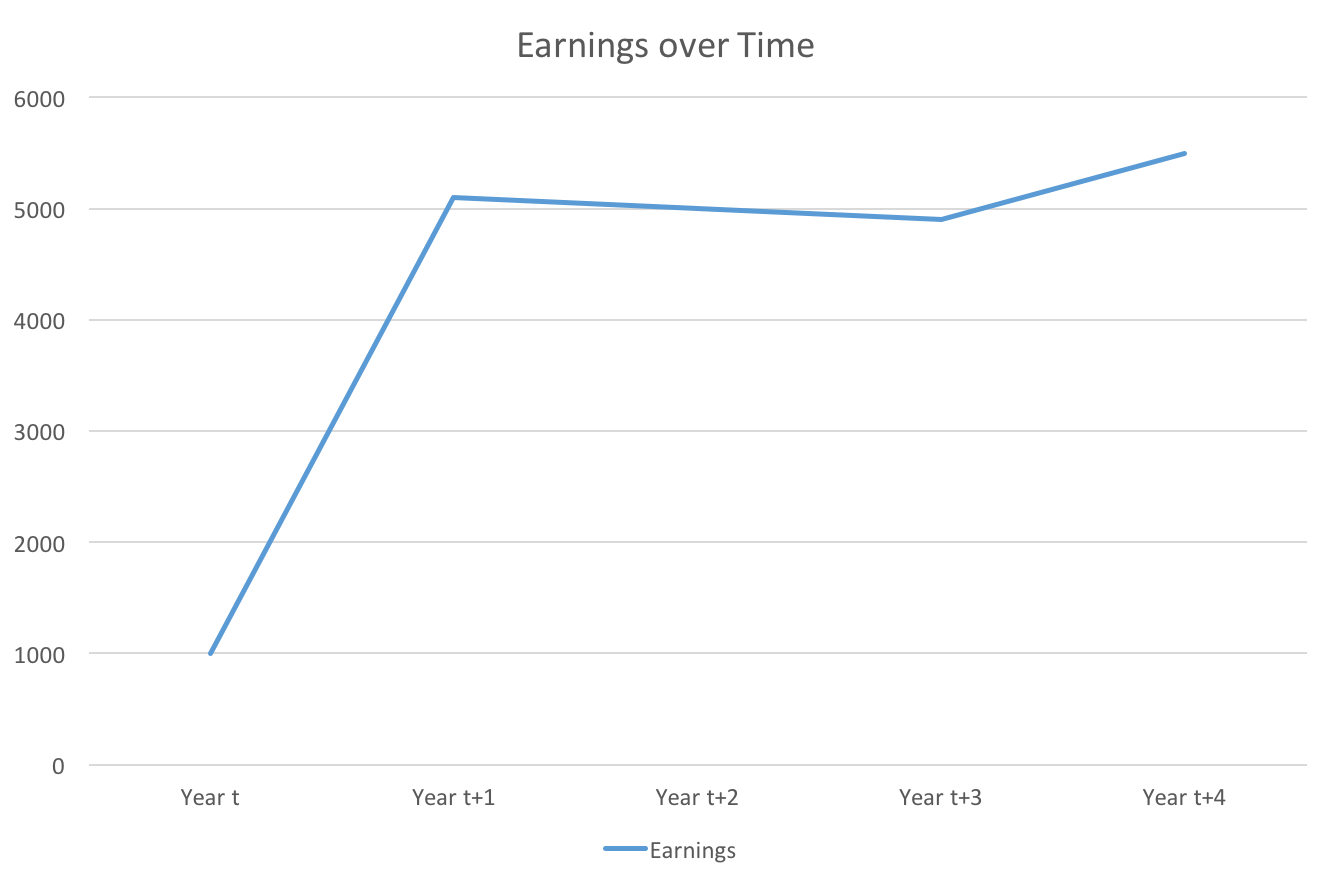
• Suppose income (earnings) is observed at Time 1 and Time 5
• No mobility
• Since individuals are not isolated, they face exogenous impacts to their income
• Will this methodology lead to correct classification and wider inference to the population?
• It is clearly too tolerant

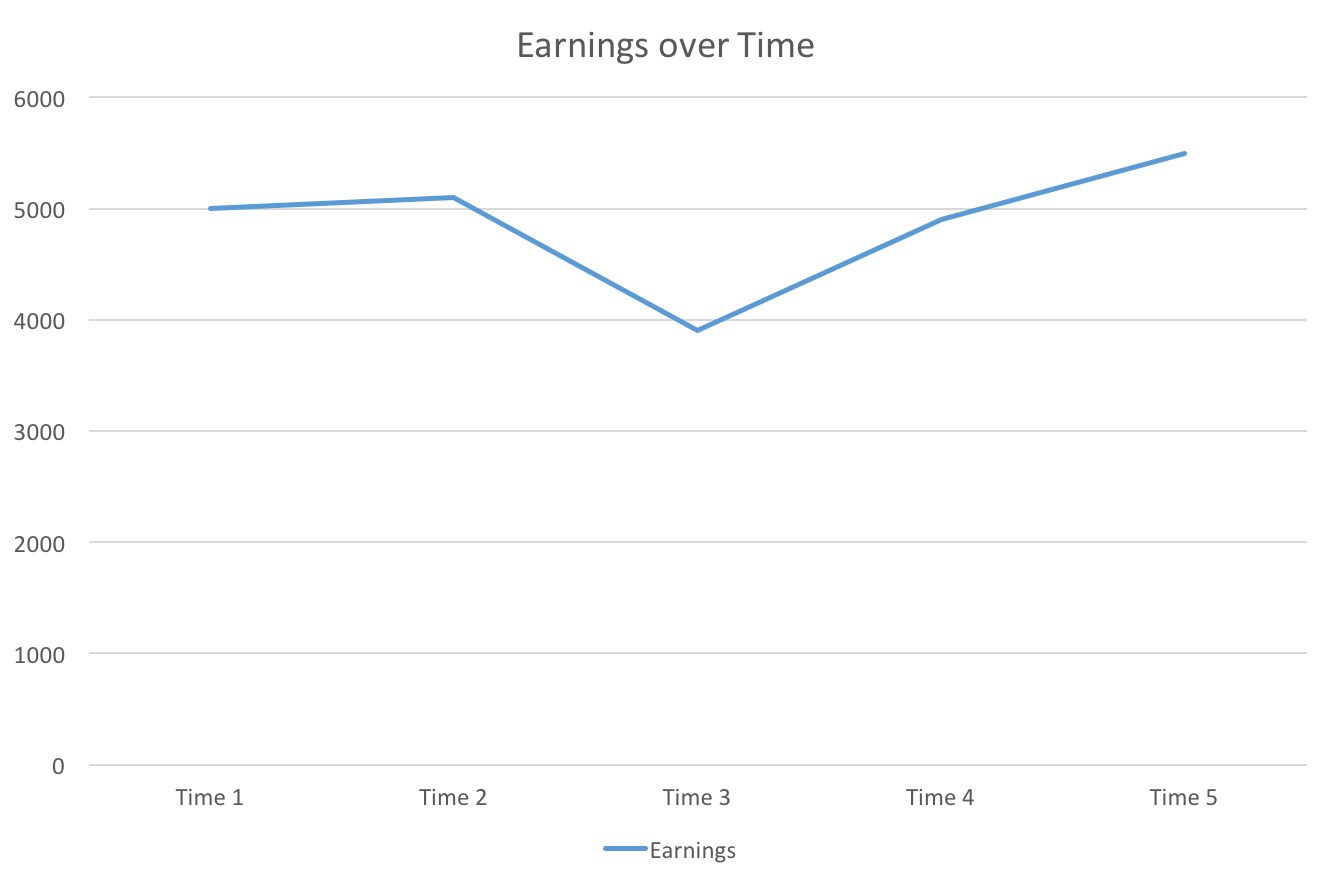
Noisy Data

• Obvious solution: use more data!
• Mobility
• This classification is too strict
• The ideal index minimizes misclassification while being tolerant enough to be robust to small exogenous income changes

Multidimensional Indices

Mobility with Respect to What?

• In multiperiod data, what rank do we evaluate mobility with respect to?
• Let $R_i$ denote this reference rank for individual $i$
• Unless there is an apriori reason to prefer a rank, use the mode
• Example: Look at individuals who joined a program thought to affect earnings at year $t$. Then $t$ ought to the be year we talk about mobility in reference to

Tolerance

• Let $\alpha$ be the tolerance parameter and $r_{it}$ be the rank of individual $i$ at time $t$
• An individual experiences mobility if $\sum_{t=1}^{N} |r_{it} - R_i| > \alpha$
• Geometrically, this is a distance to the diagonal and we can think of the set of ranks $D_\alpha = \{ r_i \mid \sum_{t=1}^{N} |r_{it} - R_i| \leq \alpha \} $ as the generalized diagonal
• Observe that the Prais-Bibby Index for arrays assumes $\alpha = 0$

Generalized Diagonal Index

• Define the Generalized Diagonal index as follows: $$m_{gd}(M_{u}) = 1 - \left( \sum_{p \in D_\alpha(M_{u})} p \right)$$
• Interpretation: probability that one is not on the Generalized Diagonal at tolerance $\alpha$

Setting Tolerance Threshold

1. $\alpha < \frac{N}{2}$
• If one does not experience mobility, then one should be in the reference rank for a majority of the observations
2. $\alpha$ is non-decreasing in $N$
• As the number of observed times increases, the tolerance threshold should never decrease

Recap

• Noisy data is problematic for multiperiod mobility measurement
• Developed the notion of tolerance to generalize the Prais-Bibby index on arrays

Empirical Analysis

Data

• Earnings data for enrollees in SNAP in Georgia during 2004
• Date range: 2004-2014
• Obtained by merging SNAP enrollment data to DOL annual wage data

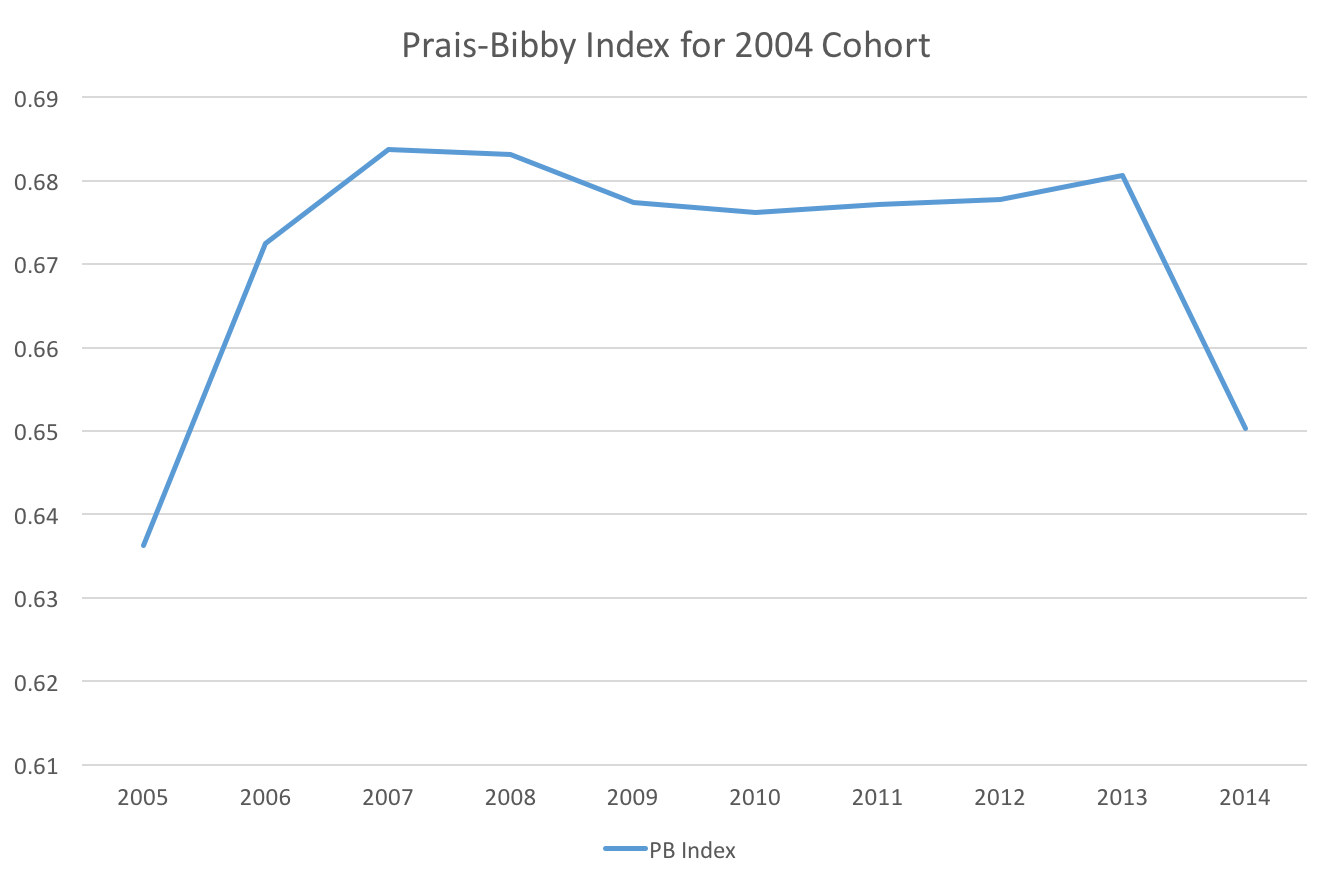
Results

• From 2006 to 2013, the Prais-Bibby index appears relatively stable
• By selecting any of these years, one may conclude that approx. 68% of the cohort experiences mobility
• This potentially includes misclassifications (additionally due to data quality issues)

Results

Conclusions

• Noisy data is problematic for multiperiod mobility measurement
• Developed the notion of tolerance to generalize the Prais-Bibby index on arrays
• Observed improvements in inferring the mobility of a population of SNAP recipients

Future Directions

• Explore the Generalized Diagonal index from the perspective of contingency tables
• Consider which sets of mobility axioms are satisfied by the Generalized Diagonal index
• Derive statistical properties of the Generalized Diagonal Index

Example