Differentially Private Query Answering and Synthetic Data
Synthetic data is data that matches the schema and domain of a given dataset as well as some of its statistical properties. This project seeks to advance methods for generating and working with tabular synthetic data under differential privacy. This problem is challenging because satisfying differential privacy limits how well the statistical properties of the original dataset are preserved in the synthetic dataset. We introduced the following methods:
- AIM (VLDB 2022), a mechanism for generating private synthetic data for discrete tabular datasets that’s state-of-the-art across several error metrics.
- JAM-PGM (AISTATS 2024), a private synthetic data mechanism that incorporates public data to reduce error and better utilize the privacy budget.
- GReM-MLE and GReM-LNN (NeurIPS 2024), two mechanisms for reconstructing answers to noisy marginals from residuals.
Topology and Explainable Machine Learning
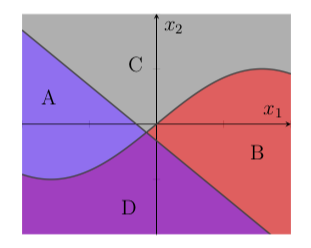
Rule-based explanations provide human-interpretable reasons for a classifier’s behavior. At the same time, rules are definable regions of the feature space. This project studies connections between the rule-based explanations of classifiers and definability in topology.
- In Fall 2021, I gave a talk at the UMass CS Theory Seminar.
- In Spring 2023, I presented a workshop paper developing the contours of this approach. We prove a result characterizing explainability as a simple topological property similar to the property of Baire.
Utterly Incomplete Look at Research
This project looks at research from years past. I survey a handful of books and articles in a particular year from math, economics, philosophy, international relations, and other interesting topics.
Current years: 1823 ∙ 1824 ∙ 1825 ∷ 1873 ∙ 1874 ∷ 1923 ∙ 1924
Infinite Cycles and the Regress Problem

This project aims to bring the work of Diestel and collaborators on infinite cycles in graphs to bear on the program of Atkinson and Peijnenburg in analyzing the justification structure of infinite chains and infinite cycles of reasoning from a probabilistic and epistemological perspective.
I presented a paper introducing this approach at the 2019 Society for Exact Philosophy conference.
Past Projects
Earnings Mobility and SNAP Participation in Georgia
This project investigated earnings mobility among SNAP participants using linked administrative data from the State of Georgia. Our goal was to better understand the earnings mobility of low-income populations and how participation in government benefits programs affects one’s earnings, especially during economic downturns such as the Great Recession.
Results from this project were presented at the National Tax Association’s Annual Conference in 2014, the Next Generation of Public Finance conference in 2016, the International Conference on Administrative Data Research in 2019, and discussed on WABE, Atlanta’s NPR affiliate, in 2017. Our findings were published in Social Science Quarterly, which utilizes an R package we developed called mobilityIndexR that can be found on CRAN.
This project was a collaboration with colleagues at the Fiscal Research Center at Georgia State University.
Updated: 06/24
