Interesting Research Programs from the 2010s
The idea of this post is to introduce and discuss several interesting research programs from the past decade. A research program (or programme) refers to a common thread of research that shares similar assumptions, methodology, etc. The list below contains a variety of research programs: some on topics that have broad appeal e.g. explainable machine learning and mental disorder; others moved the direction of entire industries e.g. advances in computer vision and cryptocurrencies; and others still are more niche areas that I happen to be deeply interested in e.g. topological learning theory, privacy attacks on ML models, and graph-theoretic approaches to epistemology.
Obviously, a list of this variety can never be complete and is surely biased by what I happen to be reading. If I’ve missed something interesting that you enjoy, let me know at brettcmullins(at)gmail.com. Enjoy!
Image Recognition and Object Detection
It is difficult for me to begin this list without first talking about the area that most affected my professional career, led to (or at least accelerated) a boom in data science, and potentially thawed an AI winter. During the 2010s, deep learning made enormous progress in heuristics and applications. For computer vision in particular, a good starting point is AlexNet in 2012 which used a convolutional neural network (CNN) architecture to substantially surpass existing benchmarks for image recognition - the task of assigning a label such as cat, dog, or tree to an image - on the ImageNet dataset. Over the next few years, improvements would continue with architectures such as VGG, ResNet, and Inception.

With progress being made with recognition, other tasks such as object detection - finding and labeling objects (sometimes multiple objects) within images - became more feasible. One approach to object detection introduced in 2013 Regional CNNs (or R-CNNs) combined a model that first produced promising bounding boxes then utilized the newly developed recognition models (starting with AlexNet) to classify or label the regions in the bounding boxes. Over the next few years, progress in this direction was realized with Fast R-CNN and Faster R-CNN. These frameworks not only employed better recognition models and found better bounding boxes, but they integrated the model components together so that they could be more efficiently trained or tailored to one’s application. Here is an excellent overview of these models with a bit more detail.
Accompanying these new techniques and improvements was a large amount of software - with TensorFlow, Caffe, and Torch at first then the more user friendly Keras - allowing anyone to implement these models for their use cases. It’s also worth mentioning the proliferation of online courses such as fast.ai’s Practical Deep Learning for Coders that facilitated getting potential users up to speed to test out and deploy these tools.
Topological Learning Theory
Topological Learning Theory is the mathematical study of the learnability/solvability of hypotheses/problems that is informed by the theory of computation and descriptive set theory rather than classical statistics (with statistical learning theory). The idea of learning theory is to analyze the learnability of hypotheses as one incrementally receives information about the true state of the world.

A classic example is to consider an ornithologist observing the color of ravens as, say, black or not. With each raven observed, the ornithologist gains information which rules out some hypotheses but is consistent with others. By coding a black raven as 1 and other ravens as 0, we can mathematically represent possible observation histories as infinite sequences of 0s and 1s, i.e. points in the Cantor space. The crux of this approach is that the topology on the Cantor space and other such spaces naturally encodes the idea of information accumulation. By considering the descriptive complexity of hypotheses, identifying a hypothesis with the set of sequences that make it true, we can say things about the learnability of the hypothesis. For instance, the hypothesis “all ravens are black” is the set containing the single sequence of all 1s. We say that this hypothesis is falsifiable since if there is a non-black raven our ornithologist will eventually observe it; however, it is verifiable not in finite time but in the limit since the hypothesis is never conclusively true after any finite number of observations. This corresponds to the topological notion of properly being an $F_{\sigma}$ or $\Sigma^{0}_{2}$ set.
Kevin Kelly’s 1996 The Logic of Reliable Inquiry has been an authoritative text on formal learning theory in the Cantor space and other Polish spaces. Advances in computable analysis beginning in the early 2000s have enabled the extension of these classical formal learning theory results to a more general topological setting throughout the 2010s. The paper Topological Properties of Concept Spaces from 2010 is the first to connect these computable analysis results to learning theory. By 2015, a pair of papers On the Solvability of Inductive Problems and Theory Choice, Theory Change, and Inductive Truth-Conduciveness - both presented at the TARK 2015 conference - provide complete topological characterizations of learnability/solvability in the limit as well as connections to belief revision theory and Ockham’s Razor in this more general topological setting.
The Disordered Mind Theory of Mental Illness
In a series of articles and books over the past decade, the philosopher George Graham develops a theory of mental disorder with the following qualities: 1. is non-reductionist with respect to the mind and the brain; 2. is informed by the philosophy of mind; and 3. coheres with the experiences of patients and clinicians. Graham’s theory holds that mental illness is distinct from somatic/bodily illness though may co-occur or otherwise be bound up with so-called broken brains. A helpful analogy for what is meant here by “the mental” or “the mind” is to view the brain as computer hardware, whereas the mind is software. On this picture, the mind and the brain are surely not independent; a hardware issue may impede the computation of some software. However, one may have bugs in one’s software - “gumming up the works” to use a common phrase of Graham - on perfectly functioning hardware.

This theory of mental disorder is developed in Graham’s text on mental illness in the context of the philosophy of mind: The Disordered Mind. A follow-up book, The Abraham Dilemma, refines this theory for the case of delusion, religious delusion in particular (I discuss The Abraham Dilemma in greater detail in my Top Books in 2020). Graham’s latest book Hearing Voices and Other Matters of the Mind explores the unique properties and challenges of mental disorders in the presence of religious content. The disordered mind theory is not without its detractors who hold that Graham goes too far in arguing that one need not situate and commit to positions in the philosophy of mind to reject the complete reduction of mental illness to neuroscience.
I took George Graham’s seminar on Philosophy and Mental Illness in 2014 at Georgia State University and had several interesting chats with him about the metaphysics and definability of mental disorders.
Machine Learning Interpretability and Explainability
The boom in data science and widespread use of machine learning models during the past decade was accelerated by innovations in model architectures as well as tools and software to train and deploy these models. In addition to the progress with neural networks and deep learning, algorithms such as XGBoost allowed users to achieve state-of-the-art classification and regression performance without much effort. XGBoost in particular became so prevalent in both industry and ML competitions - as had logistic regression and other GLMs in the past - that it was not unreasonable for some to wonder whether or not we should just use XGBoost all the time.
For all that these models gained in performance, they lost ground in being able to provide answers to questions from stakeholders, developers, and so forth when things went wrong as to why a model’s prediction was so far off or why does the computer vision model think a banana is a toaster. Two approaches were offered as a solution (three if you count “Who cares?! Let’s do nothing!”): interpretability and explanations. The former offers constraints on model building such as limiting the number of features used and restricting to linear models so that the model is sufficiently simple to allow the developer/user to reliably predict the model’s behavior with a reasonable amount of effort. The latter is a set of methods for generating reasons for a model’s behavior for arbitrarily complex models. The Mythos of Model Interpretability is an early effort to disentangle these terms and map the landscape for understanding models. Also see my attempt here as well as Christoph Molnar’s ever-evolving text Interpretable Machine Learning.
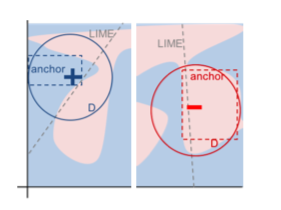
The approach that I find the most compelling stems from the LIME paper. LIME (or local interpretable model-agnostic explanations) is a method of generating an interpretable, i.e. linear, approximation of a model in the neighborhood of a given point in the feature space. This new model is then used to generate explanations by virtue of its interpretability. A second approach for classifiers called Anchors - both are developed by the same research group at UW that also developed XGBoost - produces a simple region of the feature space (a rectangle) where the model’s prediction holds with high probability for a given point. This region or anchor acts as a sort of sufficiency condition for classification. The image to the right illustrates these ideas with the dotted line being a local linear approximation and the rectangle being an anchor for points denoted by $+$ and $-$.
Part of my research studies anchors and other rule-based approaches to local explanation from a topological perspective.
The Graph-Theoretic Approach to Epistemic Justification
Formal epistemology is an area of philosophy that uses mathematical tools to study knowledge and belief. One way to represent beliefs is through directed graphs where nodes are beliefs and edges are relations of inferential support from one belief to another. For instance, for beliefs $P, Q$ we may say that there is an edge $QP$ between the beliefs for a given agent if the agent believes both $P, Q$ and $Pr(P \mid Q) > \alpha $ for some $ \alpha > 0.5$.

In a 2007 paper called Infinitism Regained, Jeanne Peijnenburg took the first steps in this literature by showing that these probabilities are well defined under some conditions for infinite chains of beliefs. This refuted a common conceptual objection against infinitism in informal epistemology. Peijnenburg along with David Atkinson published a dozen or so papers in the first half of the decade developing a theory for relating the structure of relations between beliefs to when conditional probabilities are well defined. The paper Justification by an Infinity of Conditional Probabilities is representative of this bunch. This line of research culminated in the 2017 monograph Fading Foundations which joined together their results into a coherent story with a bit more exposition than is found in the papers.
It’s worth mentioning a second thread of research in this area comes from Selim Berker’s 2015 paper Coherentism via Graphs. Berker eschews the conditional probability relations and instead develops an account which argues that complex graph structures such as hypergraphs are needed to represent the justificatory structure of beliefs.
I am currently working on applying ideas from infinite graph theory - particularly infinite cycles - to explore graph-theoretic representations of belief and implications for the regress problem. Here’s a recent talk I gave at the Society for Exact Philosophy conference.
Rethinking Academic Publishing
This entry is a bit more loosely organized than the rest and is built around a two-part series of papers: Scientific Utopia I: Opening Scientific Communication and Scientific Utopia II: Restructuring Incentives and Practices to Promote Truth Over Publishability. Part I presents a decentralized vision for communicating scientific results and offers steps to reach this state such as allowing open access to all published papers (with a model similar to arXiv) as well as making peer reviews and commentary on research articles widely available. Regarding the latter, the authors stress that these contributions often go unacknowledged and unrewarded. In A World Without Referees, Larry Wasserman counters a common objection to this vision:
“if there does end up being a flood of papers then smart, enterprising people will respond by creating websites and blogs that tell you what’s out there, review papers, etc. That’s a much more open, democratic approach.”
Part II surveys approaches taken to make published statistical results more reliable and offers additional measures such as registering study protocols before collecting data, lowering the barriers to publishing, and making sharing data the norm (when it is feasible). This is especially prescient given the reproducibility crisis and methodological critiques such as Gelman and Loken’s Garden of Forking Paths. While there has been progress, it’s not yet clear what the future of publishing statistical analyses will and ought to look like.
Privacy Attacks on Machine Learning Models
Privacy attacks refer to cases in which an adversary attempts to learn information about a machine learning model given access to the model. Adversaries may have varying degrees of access to a model. For instance, one may recover the coefficients of a linear model from a publish paper or software documentation and know the full model or one may be able to call a API to score data if a model is deployed as a SaaS product.
But what information about models could adversaries try to learn? Model inversion attacks attempt to recreate parts of the training data or to learn sensitive attributes for a given record. Privacy in Pharmacogenetics: An End-to-End Case Study of Personalized Warfarin Dosing from 2014 introduces an approach to learn sensitive information about a person such as whether or not they have such-and-such genetic marker from pharmacogenetic models that predict something observable - in this case, one’s optimal Warfarin dosage - from genetic markers and demographic information. On the security side, the authors discuss the prospect of using differential privacy to defend against such attacks.
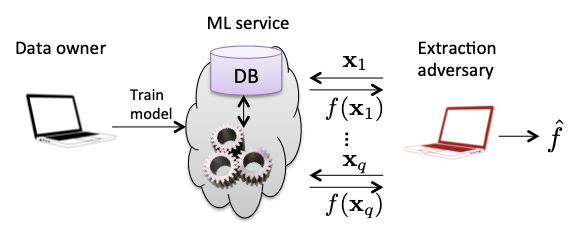
Model Extraction attacks attempt to reconstruct the model from partial information. Stealing Machine Learning Models via Prediction APIs from 2016 introduces methods to reconstruct linear models and decision trees - in some cases a completely accurate reconstruction - in the case of classifiers where confidence scores are provided to the adversary in addition to the label on a query. Property Inference attacks seek to learn aggregate properties of the training data that are not explicitly encoded in the data itself. Hacking Smart Machines with Smarter Ones from 2015 develops an attack in the context of speech recognition - the task of transcribing audio to text - to predict whether or not a given model was trained using recordings with an Indian-American accent, a property that may not and likely is not explicitly noted.
Current research in this area looks at ways to formalize these attacks to better understand both the related security properties of various sorts of machine learning models and how to generally defend against these attacks.
Blockchains and Cryptocurrencies
I couldn’t end this list without touching on the bandwagon spectacular that is/was Bitcoin, blockchains, and the cryptocurrency ecosystem. For a brief period, news about trading cryptocurrencies and such-and-such company’s new blockchain initiative was smothering. I’m sure everyone had that colleague that was skimping on their lunches and deferring their student loans to fuel their portfolio with Ethereum Tokens and Bitcoin futures.

Rather than technical innovations and what-not, I’m much more interested in the cultural aspects of this phenomenon. David Gerard’s Attack of the 50 Foot Blockchain (also found in my Top Books in 2018) and blog of the same title have been invaluable resources for learning about and documenting cryptocurrency culture with its cypherpunk origins and continual chicanery and shenanigans.
I also want to point you to Kai Stinchcombe’s hot takes (or rather cold water) on blockchain as a practical technology that companies could build into their products or that could be utilized at scale in society.
One positive outcome of the blockchain boom - that I gained from and hope others did as well - is exposure to new ideas and challenges. In my case, these include troubleshooting hardware issues such as having to use a screwdriver as the power button for a mining rig, fiddling with GPUs and load balancers (which was fashionable given the coinciding progress in deep learning), and absorbing a bit of cryptography along the way.
 Buy me a coffee
Buy me a coffee
